Zur Wiederholung: Eine Funktionskomposition entsteht dann, wenn
man z.B. bei einer Funktion ![]() anstatt der unabhängigen Variable
anstatt der unabhängigen Variable
![]() eine weitere Funktion von ebenderselben Variablen, z.B.
eine weitere Funktion von ebenderselben Variablen, z.B. ![]() einzusetzen, die resultierende Funktion lautet dann z.B.
einzusetzen, die resultierende Funktion lautet dann z.B. ![]() .
Natuerlich muß dabei gegeben sein, daß der Wertebereich von
.
Natuerlich muß dabei gegeben sein, daß der Wertebereich von ![]() eine Teilmenge des Definitionsbereiches von
eine Teilmenge des Definitionsbereiches von ![]() ist. Gilt z.B.:
ist. Gilt z.B.:
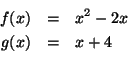
dann ist
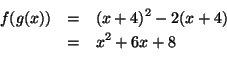
Übertragen wir dies Prinzip auf unsere Wellentafeloszillatoren, so
ist folgende Schaltung denkbar: Ein Oszillator, liest eine Wellentafel
aus (![]() )). Die so erhaltenen Werte werden nun nicht direkt
als Audiosignale genutzt, sondern dienen, entsprechend skaliert, als
Index in eine weitere Wellentafel. So erhalten wir ohne großen
Aufwand
)). Die so erhaltenen Werte werden nun nicht direkt
als Audiosignale genutzt, sondern dienen, entsprechend skaliert, als
Index in eine weitere Wellentafel. So erhalten wir ohne großen
Aufwand ![]() .
.
Waveshaping beschäftigt sich jetzt damit, nützliche Funktionen zu finden, die eine Wellenform als Argument akzeptieren und diese in klanglich interessanter Form modifizieren. Diese Funktion nennt man dann die Transfer Funktion.
Abbildung 4.1 zeigt das Bild für
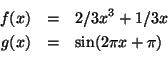
und
An dem man gut die nichtlineare Verzerrung des Eingangssignals sehen kann. Das Ausgangssignal ist hier kein Sinus mehr, enthält also mehr Obertöne als das Eingangssignal.