Mathematische Grundlagen

Rein technisch geschieht Waveshaping nun so, daß man ein beliebiges Signal nimmt, und dies jetzt als Index in eine vorberechnete Tabelle benutzt. Die Tabelle stellt dabei die Transferfunktion $f(x)$ dar, das Signal die Eingangsfunktion $g(x)$.

Es gibt keine allgemeine Theorie, wie das Spektrum des Ausgangssignals aus Eingangssignal und Transferfunktion herzuleiten ist. Es gibt jedoch eine Klasse von Funktionen, bei denen man zumindest bei einer Amplitude des Eingangssignals von 1 sagen kann, welches Resultat entsteht, nämlich die sogenannten Chebyshev Polynome erster Art.

Mathematisch sind Chebyshev Polynome Lösungen der Differentialgleichung

$$(1-x^2)y'' - xy' +n^2y = 0$$

Ohne näher auf die Geheimnisse der Differentialgleichungen einzugehen sei vermerkt, daß Lösungen dieser Gleichung Chebyshev Polynome erster Ordnung sind, die durch

$$T_n(x)=\cos(n\cos^-1x)$$

gegeben sind. Chebychev-Polynome kann man durch folgende Gleichung auseinander herleiten, wobei gilt:

$$T_{n+1}(x)=2xT_n(x)-T_{n-1}(x)$$

wobei die ersten Chebychev-Polynome gegeben sind als

$$\begin{eqnarray*} T_0(x)&=&1\\ T_1(x)&=&x\\ T_2(x)&=&2x^2-1\\ T_0(x)&=&4x^3-3x\\ \end{eqnarray*}$$

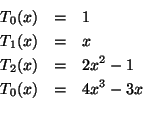
Setzt man für $x$ jetzt $\cos x$ in die Gleichungen ein, so erhält man nach entsprechender Umformung die folgende nette Gleichung:

$$T_k\cos x = \cos kx$$

D.h: Liest man mit den Werten einer Cosinusfinktion ein Chebychev-Polynom $T_k$ aus, erhalt man als Resultat einen die $k$-te Harmonische der Eingangsfrequenz. Da die Skalierung und Addition von Funktionen eine lineare Operation ist, kann man also auch Chebychev Polynome beliebig addieren und Skalieren.

Nimmt man also als Transferfunktion z.B.

$$3T_1(x) + 1.5T_4(x) + 0.1T_9(x)$$

So erhält man als Ergebnis des o.g. Waveshapingprozesses ein Signal mit Grundton, 4. und 9. Teilton, im Amplitudenverhältnis 3:1.5:0.1.

Nun ist es so, und das ist das interessante beim Waveshaping, daß man, wenn man das Waveshaping mit einer Amplitude $<0$ betreibt, keineswegs ein Spektrum erhält, das in irgendeinerweise linear von Anfangs- und Endspektrum abhinge. Im Gegenteil: Obertöne, die im Endspektrum gar nicht auftauchen, erscheinen zwischendurch, und verschwinden wieder, solche, die im Endspektrum kaum vorhanden sind sind zwischendurch penetrant vorhanden usw. Das einzige, was man generell sagen kann ist, das je näher die Amplitude bei 1 liegt, desto mehr höhere Harmonische können ins Spiel kommen. Je mehr die Amplitude bei 0 liegt, desto mehr ähnelt das Ausgangssignal dem Eingangssignal.

Die Amplitude des Eingangssignals dient also auch als Indikator für den Obertongehalt des Spektrums (immer bezogen auf Chebychev-Polynome als Transferfunktionen). Dies Verhalten ähnelt dem von akustischen Instrumenten, die ein mehr an zugeführter Energie häufig auch in eine (durchaus nicht-lineare) Erweiterung des Spektrums umsetzen.

Oft will man aber Amplitude und Spektrum getrennt voneinander kontrollieren. Dazu muß man dann zunächst das geshapete Signal wieder auf Normpegel bringen, um es dann den normalen Amplitudenmanipulationen zu unterwerfen.